NNLM——A Neural Probabilistic Language Model
1 基础概念
统计语言模型
- 建立统计语言模型就是学习一个单词序列的联合概率分布
维数灾难(curse of dimensionality)
- 测试用的语句和训练用的语句很可能完全不同
- 尤其容易出现在训练离散的、随机的变量的联合分布的时候
SOTA、Baseline、Benchmark
- SOTA 全称是 state of the art,是指在特定任务中目前表现最好的方法或模型。Benchmark和baseline都是指最基础的比较对象。
- 你论文的 motivation 来自于想超越现有的 baseline/benchmark,你的实验数据都需要以 baseline/benckmark 为基准来判断是否有提高。唯一的区别就是baseline讲究一套方法,而 benchmark 更偏向于一个目前最高的指标,比如 precision、recall 等等可量化的指标
- 举个例子,NLP 任务中 BERT 是目前的 SOTA,你有 idea 可以超过 BERT。那在论文中的实验部分你的方法需要比较的 baseline 就是 BERT,而需要比较的 benchmark 就是 BERT 具体的各项指标
语言模型常用评价方法——perlexity、BLEU
- 语言模型常用评价方法:perplexity、bleu_满腹的小不甘静静的博客-CSDN博客
在语言模型的训练中,通常使用perplexity的对数形式——将每个位置上的概率取对数再平均:
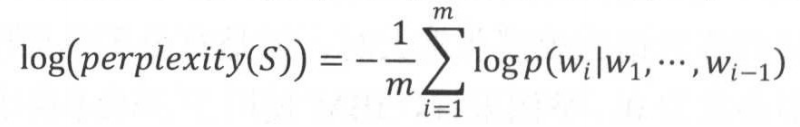
词向量
- 目的:使计算机通过词向量获取的信息和人类通过文本看到的信息一致
- 最早的词向量:one-hot
- 带来维度灾难和语义鸿沟的问题
- 这种情况下,词表越大,维度随之变大,会使样本稀疏——带来维度灾难
- one-hot 产生的向量彼此正交,不能体现出它们之间的相似性大小——带来语义鸿沟
2 Abs & Conclu & Introduction
2.1 动机、与 SOTA 的对比
- 动机:解决维度灾难的问题,使统计语言建模获得更好的泛化(generalization)
- SOTA:n-gram 模型
- 如何获得泛化能力:合并训练集中一些短的重复出现的序列,放入一个词袋中
- 缺点:
- 对上下文的利用不够好,只能使用 1-2 个距离的词语
- 没有考虑词语之间的相似度
- The cat is walking in the bedroom VS. A dog was running in a room
- 猫和狗从语义上应该是接近的,学习了前一个句子,就应该明白后一个句子
- n-gram 没有考虑到这一点
- 泛化能力不够强
- 对于训练集中没有出现过的 n 元组条件概率为 0 的情况,只能用平滑法或者回退法赋予它们概率
- 论文提出一个新的模型 NNLM
- 学习以下两个内容:
- 每个单词的分布式表示
- 用“分布式表示”所展现出的单词序列的概率函数
- 如何获得泛化能力:一个从未出现过的句子如果和已经出现的句子具有相似的语义信息也可以获得高概率
- 优点:对上下文的利用更好,考虑了词语之间的相似度
- 缺点:训练起来困难
- 学习以下两个内容:
2.2 普适于语言领域的条件概率模型
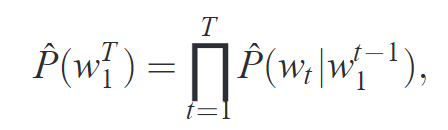
- $w_t$ is the $t$-th word,and writing sub-sequence $w_i^j= ( w_i,w_{i+1},···,w_{j−1},w_j )$。
- 在这些领域被证实有用:speech recognition, language translation, and information retrieval
- 因此,对这个模型的改善能够影响许多应用
2.3 n-gram 简介
- n-gram models construct tables of conditional probabilities for the next word, for each one of a large number of contexts
- 基本思想:将文本里面的内容按照字节进行大小为 n 的滑动窗口操作,形成了长度是 n 的字节片段序列
- 每一个字节片段称为 gram,对所有 gram 的出现频度进行统计,并且按照事先设定好的阈值进行过滤,形成关键 gram 列表,也就是这个文本的向量特征空间,列表中的每一种 gram 就是一个特征向量维度。
- 该模型基于这样一种假设:第 t 个词的出现只与前面 n-1 个词相关,而与其它任何词都不相关,整句的概率就是各个词出现概率的乘积。这些概率可以通过直接从语料中统计 n 个词同时出现的次数得到
- 常用的是二元的 Bi-Gram 和三元的 Tri-Gram。
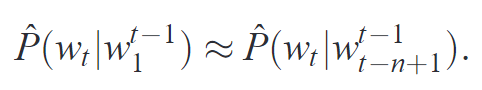
2.4 论文模型简介

- 特征向量
- 代表单词的很多方面(维度),每个单词在向量空间中都表现为一个点
- 特征向量之间的联系需要学习,但是也可以使用先验知识来建立
- 特征的数量(实验中为 30、60、100)远远小于词典的大小(17000)
- 概率函数:已知前一个单词,后一个单词出现的条件概率的乘积(联合gai’l’c)
- 联合概率分解为条件概率的乘积
- 该函数具有可迭代调整的参数,以便最大化训练数据的对数似然或正则化准则,例如通过添加权重衰减惩罚
- 概率函数是一个光滑的函数,因此,某一个特征的微小改变都会带来概率的微小变化
- 光滑函数(smooth function)是指在其定义域内无穷阶数连续可导的函数。
- 也就是说概率函数对特征变化非常灵敏,从而,训练集中存在一群意思相近的句子中的一个,就可以训练到这一群句子
3 A Neural Model
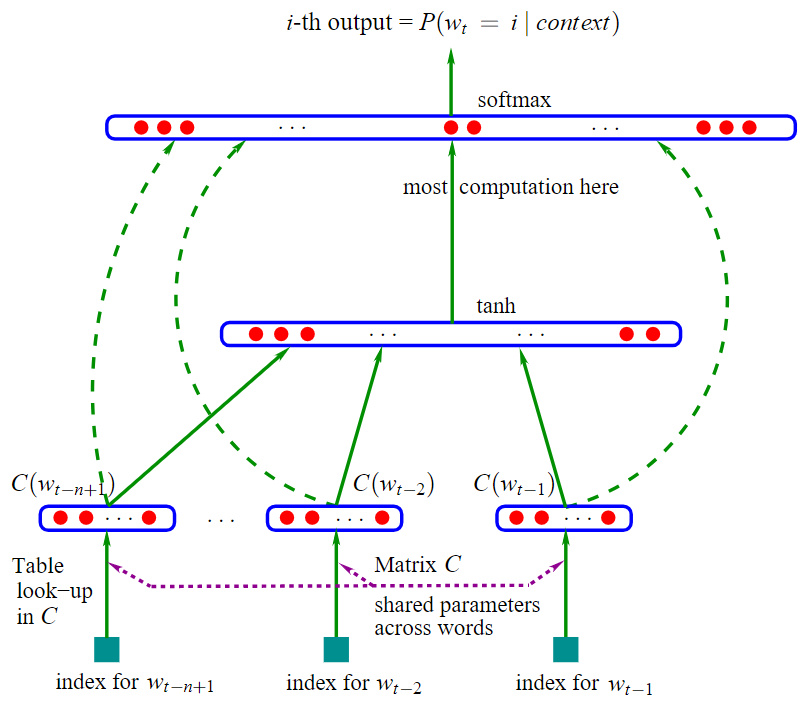
3.1 模型基本架构
- 使用了 MLP 构建语言模型
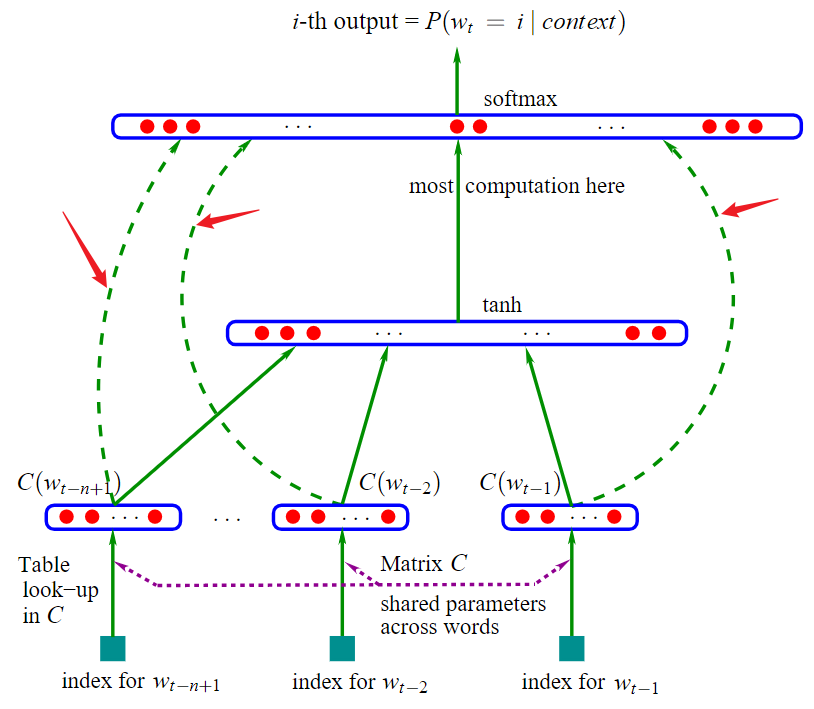
- 模型一共三层:
- 第一层是映射层,将 n 个单词映射为对应 word embeddings 的拼接,其实这一层就是 MLP 的输入层
- 第二层是隐藏层,激活函数用 tanh
- 第三层是输出层,因为是语言模型,需要根据前 n 个单词预测下一个单词,所以是一个多分类器,用 softmax
- 计算瓶颈:
- 整个模型最大的计算量集中在最后一层上,因为一般来说词汇表都很大,需要计算每个单词的条件概率,计算量可想而知
- softmax 是很低效的,此后出现了很多优化,比如层级 softmax、softmax tree 等。
- 结构的优化:
- 用 RNN 替代 MLP:Tomas Mikolov 提出的 RNNLM
3.2 训练集
- 一个词序列 $w_1,…,w_T$
- 其中 $w_t∈V$$w_t$ 表示词序列的第 $t$ 个词
- $V$ 是单词表,是一个非常大但是有限的集合
3.3 核心函数
- $f\left(w_{t}, \cdots, w_{t-n+1}\right)=\hat{P}\left(w_{t} \mid w_{1}^{t-1}\right)$
- 和 N-gram 类似,NNLM 也假设当前词仅依赖于前 n-1 个词,因此函数输入为当前词和它之前 n-1 个词
- 函数意义:在给定词序列 $w_1,\cdots ,w_{t-1}$ 的条件下,下一个词是 $w_t$ 的概率
- 约束条件
- $\sum_{i=1}^{|V|} f\left(i, w_{t-1}, \cdots, w_{t-n+1}\right)=1$
- $f(w_t, w_{t-1}, \cdots, w_{t-n+1}) > 0$
- 即:给定一个单词序列 $w_1^{t-1}$,预测下一个词是 $i$ 的概率,$i$ 是词表 $V$ 中的单词,这些概率之和为 $1$,且每一个概率值均大于 0
- 函数实现:将这个函数分成两部分
- $f\left(i, w_{t-1}, \cdots, w_{t-n+1}\right)=g\left(i, C\left(w_{t-1}\right), \cdots, C\left(w_{t-n+1}\right)\right)$
- 函数 $C(i)$:将词表 $V$ 中的单词 $i$ 映射为分布式向量表示(distributed feature vectors)
- 实际上 $C$ 是一个 $|V|m$ 的*参数矩阵,矩阵的第 $i$ 行是单词 $i$ 的词向量,$C(i)∈R^m$
- $m$ 为词向量的维度
- 函数 $C$ 的参数就是矩阵本身
- 对应输入层
- 实际上 $C$ 是一个 $|V|m$ 的*参数矩阵,矩阵的第 $i$ 行是单词 $i$ 的词向量,$C(i)∈R^m$
- 函数 $g$:将词向量表示的输入序列 $\left(C\left(w_{t-n+1}\right), \ldots, C\left(w_{t-1}\right)\right)$ 映射成预测下一个词的概率分布 $\hat{P}\left(w_{t} \mid w_{1}^{t-1}\right)$
- $g$ 的输出是一个向量,向量的第 $i$ 个值代表下一个词是 $i$ 的概率
- 函数 $g$ 可以是前馈神经网络、卷积神经网络、参数化函数(参数为 $\omega$)
- 对应隐藏层和输出层
3.4 g 函数(隐藏层和输出层)的实现
- $y=b+W x+U \tanh (d+H x)$
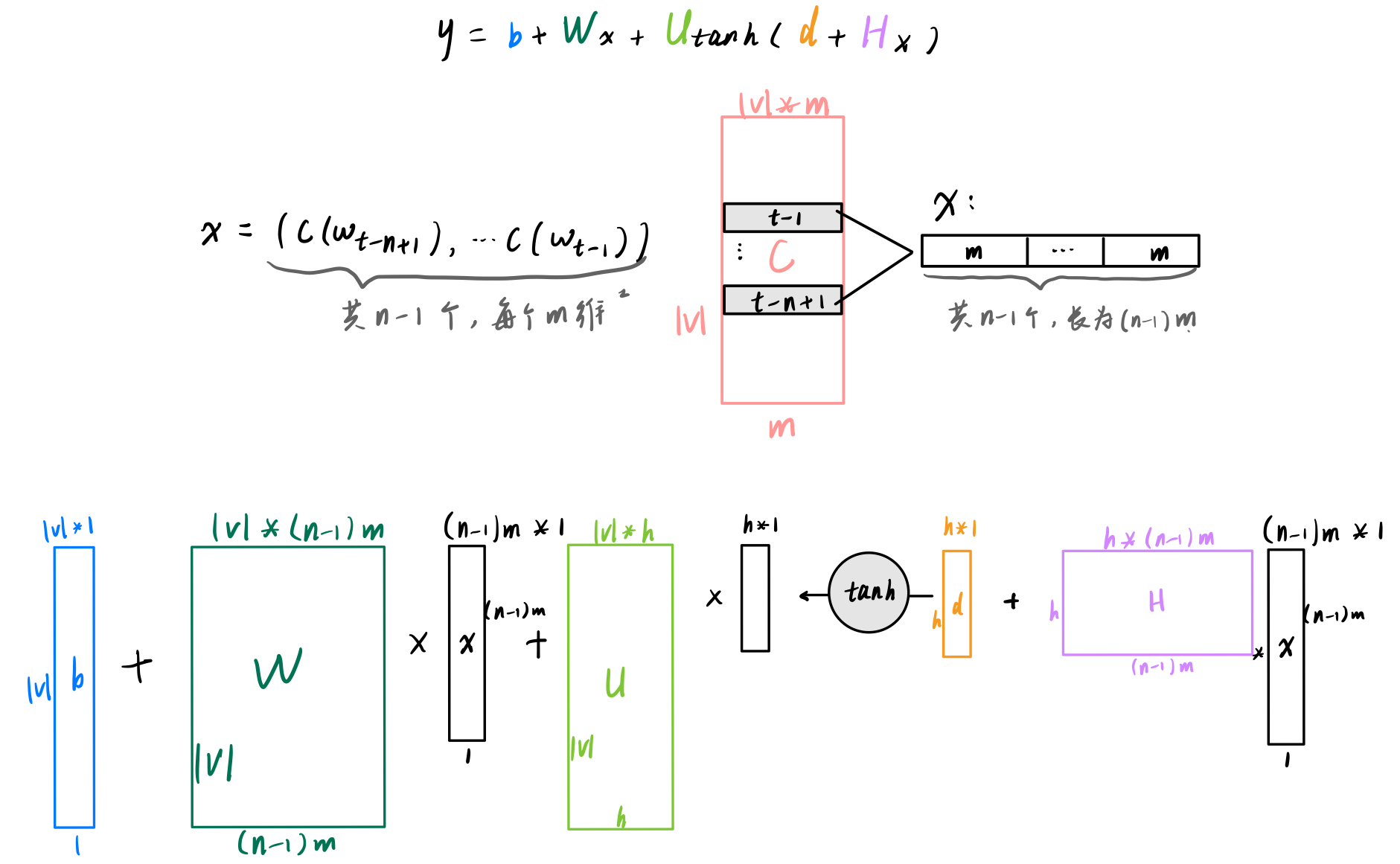
$x$ 是词向量表示的单词序列:$x=\left(C\left(w_{t-n+1}\right), \ldots, C\left(w_{t-1}\right)\right)$
$\tanh$ 是激活函数,$\tanh (d+H x)$ 是隐藏层
$b$、$W$、$U$、$d$、$H$ 都是参数
$b$ 是输出偏移,是 $|V|*1$ 的向量
$d$ 是隐藏层偏移,是 $h*1$ 的向量($h$ 是隐藏单元的数量)
$U$ 是隐藏层 ⇒ 输出层的权重,是一个 $|V| * h$ 的矩阵
$W$ 是词向量 ⇒ 输出层的权重,是一个 $|V| * (n-1)m$ 的矩阵
当 $W$ 为 $0$ 时,即 $x$ 不会直连到 $y$,对应到架构图就是三条绿色的虚箭头消失(下图红色箭头所指的)
$H$ 是隐藏层权重,是一个 $h*(n-1)m$ 的矩阵
输出的 $y$ 是一个一维向量,表示给定单词序列的条件下,下一个单词是 $y_i$ 的概率
- 输出层:上述公式输出的 $y$ 没有进行归一化,因此使用 softmax 归一化,如下
- $\hat{P}\left(w_{t} \mid w_{t-1}, \cdots w_{t-n+1}\right)=\frac{e^{y_{w_{t}}}}{\sum_{i} e^{y_{i}}}$
3.5 训练
- 由上述可以确定参数集合
- 训练过程就是找 $\theta$,使得训练集的对数似然函数最大化:$L=\frac{1}{T} \sum_{t} \log f\left(w_{t}, w_{t-1}, \cdots, w_{t-n+1} ; \theta\right)+R(\theta)$
- $R(θ)$ 为正则项
- 采用随机梯度上升法进行训练:$\theta \leftarrow \theta+\varepsilon \frac{\partial \log \hat{P}\left(w_{t} \mid w_{t-1}, \cdots w_{t-n+1}\right)}{\partial \theta}$